Test Suite for Astrophysical Code Comparison

Static Cluster Test

Both this test and the translating cluster test move away from fluid instabilities to test how the code deals with gravity. A self-gravitating gas, where every fluid element affects every other, is a vastly complex situation but one which few Astrophysics simulations can be performed without. In these tests, there are no analytical expressions that can be calculated for comparison, but we choose situations where the end result is nevertheless known. In this test, the cluster is set up with no bulk velocity and we test whether the code can ensure it remains balanced in hydrostatic equilibrium.

Initial conditions

The model used for the galaxy cluster is the King model (King 1966; Padmanabhan 2002), which was chosen because it possesses a finite radial cut-off, and is therefore a well defined problem for a code comparison. Its form is based on the distribution function:

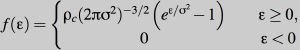
where &epsilon = &Psi - 1/2 v², is the coordinate change for the shifted energy, &rho_c is the central density and &sigma is related to (but not equal to) the velocity dispersion. The resulting density distribution of this cluster vanishes at the tidal radius, r_t.Integrating over all velocities yields a density distribution:

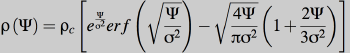
Putting this into the Poisson equation results in a second order ODE which can be solved numerically. A c code that does this can be found [here]. This model has three independent parameters, the mass of the cluster, the tidal radius and the concentration c = log₁₀(rt/r0), where r₀ is the central or King radius. For this problem, we selected a concentration of 3, r_t = 1Mpc and a cluster mass of 1014 M_solar. This results in a King radius of 1 kpc. Therefore, to successfully maintain hydrostatic equilibrium, the codes must be able to model the cluster out to 1Mpc while resolving the 1 kpc core. The profile of the cluster is analyzed at t = 1 Gyr.

Code Specifics

For the results presented below, Enzo was run with an initial grid of 100³ and eight additional levels of refinement, each reducing the cell size by a factor of two. These subgrids were placed anywhere where the cell mass was above a critical value. The cluster was set up in a box of size 3Mpc with isolated gravitational boundary conditions. This gave a minimum cell size in the core of 0.12 kpc. Flash ran with the same boxsize and with periodic boundary conditions. It used a slightly larger initial grid of 128³ and included seven additional levels of refinement, each of which reduced the cell size by a factor of two. This gave a minimum cell size in the core of 0.18 kpc. Hydra and Gadget2 radially perturbed a glass of 100,000 particles to the desired density profile within a periodic 3Mpc box.

A quantitative test suite for codes used in Astrophysics

Initial conditions

Code Specifics

Results