

Следующий: 2. Образование молекулярных облаков
Вверх: 1. Сверхоболочки в нашей
Предыдущий: 1.1 Наблюдательные данные
В настоящее время для объяснения происхождения расширяющихся
сверхоболочек нейтрального водорода привлекаются два
различных механизма.
- Оболочки -- продукт эволюции OB-ассоциаций. Впервые
этот механизм был предложен Брувейлером [8] и Томисакой и
Икеучи [66]. В их модели первоначальный ``пузырь''
(bubble) в газовом диске выдувается звездным ветром самых
массивных звезд молодой ОВ-ассоциации -- звезд класса О.
Эволюция оболочки может быть описана на этой стадии решением
Уивера и др. [72]. Затем, когда О-звезды заканчивают свою
эволюцию, включается новый источник энергии -- повторяющиеся
вспышки сверхновых все меньших и меньших масс. На этой стадии
для описания эволюции оболочки Брувейлер [8] использовал
только законы сохранения массы и импульса:
| |
|
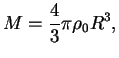 |
(1.1) |
| |
|
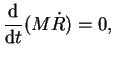 |
(1.2) |
и не учитывал давления горячего ионизированного
газа, находящегося внутри оболочки. Поэтому полученные им
размеры и скорости расширения оболочек недооценены. Томисака и
Икеучи [66] провели численные расчеты для сферических
оболочек уже с учетом внутреннего давления горячего газа.
Сверхновые в их модели вспыхивали по одной, с интервалом от
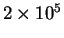 до
до 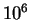 лет. Считалось, что оболочка
прекращает свою эволюцию распадаясь на отдельные фрагменты,
когда ее скорость сравнивается со скоростью звука в окружающем
газе
лет. Считалось, что оболочка
прекращает свою эволюцию распадаясь на отдельные фрагменты,
когда ее скорость сравнивается со скоростью звука в окружающем
газе 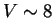 км/с.
км/с.
- Столкновения с плотным газовым диском галактики
высокоскоростных компактных облаков нейтрального водорода.
Скорости таких облаков достигают 400 км/с. Тенорио-Таглэ и
др. [65] показали, что при таком механизме для
образования наибольших наблюдаемых оболочек (с
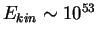 эрг) необходимы столкновения с газовым галактическим
диском очень плотных (с поверхностной плотностью
эрг) необходимы столкновения с газовым галактическим
диском очень плотных (с поверхностной плотностью
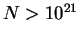 см
см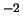 ) и массивных (с массой
) и массивных (с массой
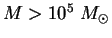 ) облаков (при скорости падения 100 км/с). А
это типичные параметры гигантских молекулярных облаков (ГМО),
которые являются центрами звездообразования.
) облаков (при скорости падения 100 км/с). А
это типичные параметры гигантских молекулярных облаков (ГМО),
которые являются центрами звездообразования.
Из этих двух механизмов более привлекательным
представляется первый.
Маккрэй и Кафатос [45] показали, что при расчетах
эволюции оболочек дискретные вспышки сверхновых можно заменить
квазинепрерывным источником энергии, причем для типичных
ОВ-ассоциаций мощность такого источника в течении большей части
жизни оболочки остается практически неизменной. Численно она
может быть оценена как [45]:
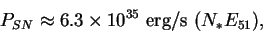 |
(1.3) |
где 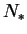 -- число звезд в ассоциации массивнее
-- число звезд в ассоциации массивнее
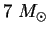 ,
,
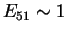 -- полная энергия, выделяющаяся при
одной вспышке сверхновой (в единицах
-- полная энергия, выделяющаяся при
одной вспышке сверхновой (в единицах 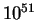 эрг). Типичная
ОВ-ассоциация содержит 20 - 40 звезд класса ранее В3 в
области с размерами, меньшими 100 пс, однако встречаются
ассоциации, содержащие до сотен таких звезд [45]. Звезды
класса О существуют около 5 млн. лет, класса В3 -- 50 млн.
лет. Отсюда следует, что на ранних стадиях эволюции самым
мощным источником энергии является звездный ветер от О-звезд,
а в последующие 30 - 50 млн. лет -- последовательные вспышки
сверхновых.
эрг). Типичная
ОВ-ассоциация содержит 20 - 40 звезд класса ранее В3 в
области с размерами, меньшими 100 пс, однако встречаются
ассоциации, содержащие до сотен таких звезд [45]. Звезды
класса О существуют около 5 млн. лет, класса В3 -- 50 млн.
лет. Отсюда следует, что на ранних стадиях эволюции самым
мощным источником энергии является звездный ветер от О-звезд,
а в последующие 30 - 50 млн. лет -- последовательные вспышки
сверхновых.
Размеры самых крупных оболочек превышают 1 кпc, что
значительно больше масштаба неоднородности газового диска
Галактики (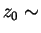 100 - 300 пc). Также необходим учет
100 - 300 пc). Также необходим учет
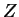 -компоненты гравитационного поля Галактики. Очевидно, что
для построения более правдоподобных моделей эволюции оболочек
необходимы двумерные алгоритмы.
-компоненты гравитационного поля Галактики. Очевидно, что
для построения более правдоподобных моделей эволюции оболочек
необходимы двумерные алгоритмы.
Отдельно роли неоднородности газа по 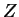 -координате и
дифференциальности вращения галактического диска
рассматривались ранее многими
авторами [67,64,40,42,41,32,52,65,83]. Первые полные
двумерные расчеты эволюции оболочек в среде, неоднородной по
-координате и
дифференциальности вращения галактического диска
рассматривались ранее многими
авторами [67,64,40,42,41,32,52,65,83]. Первые полные
двумерные расчеты эволюции оболочек в среде, неоднородной по
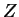 -координате, провели Томисака и Икеучи [67]. Они
рассматривали равновесный (
-координате, провели Томисака и Икеучи [67]. Они
рассматривали равновесный (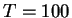 К) газовый слой с
распределением плотности:
К) газовый слой с
распределением плотности:
![\begin{displaymath}
n(z) = n_0 \left\{ 0.22 \exp \left[ -\frac{\Phi(z)}{\sigma_...
... 0.78 \exp \left[ -\frac{\Phi(z)}{\sigma_c^2}\right]
\right\}
\end{displaymath}](img77.gif) |
(1.4) |
и гравитационным потенциалом звездного диска
![\begin{displaymath}
\Phi (z) = 68.6 \ln \left[ 1+0.9565 \:{\rm sh}^2 \left(0.758
\frac{z}{z_0}\right) \right] \mbox{km}^2/\mbox{c}^2,
\end{displaymath}](img78.gif) |
(1.5) |
где дисперсии скоростей межоблачной среды и облаков
равны соответственно 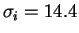 км/с и
км/с и
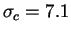 км/с, а характерный масштаб неоднородности
км/с, а характерный масштаб неоднородности
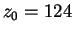 пс. Предполагалось, что вспышки сверхновых
обеспечивают постоянный приток энергии в полость с мощностью
пс. Предполагалось, что вспышки сверхновых
обеспечивают постоянный приток энергии в полость с мощностью
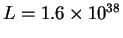 эрг/с. Мак Лоу и Маккрэй [40] для
решения аналогичной задачи использовали приближение тонкого
слоя. Мак Лоу и др. [42,41] провели полные двумерные
расчеты эволюции оболочек в стратифицированной среде.
Полученные решения с высокой точностью следуют аналитическим
уравнениям Уивера и др. [72]. Они также очень хорошо
согласуются с результатами Мак Лоу и Маккрэя [40],
полученными в приближении тонкого слоя. Таким образом, данное
приближение может с успехом использоваться при расчетах
движения ударных волн в неоднородных средах.
эрг/с. Мак Лоу и Маккрэй [40] для
решения аналогичной задачи использовали приближение тонкого
слоя. Мак Лоу и др. [42,41] провели полные двумерные
расчеты эволюции оболочек в стратифицированной среде.
Полученные решения с высокой точностью следуют аналитическим
уравнениям Уивера и др. [72]. Они также очень хорошо
согласуются с результатами Мак Лоу и Маккрэя [40],
полученными в приближении тонкого слоя. Таким образом, данное
приближение может с успехом использоваться при расчетах
движения ударных волн в неоднородных средах.
Расчеты показывают, что оболочки, расширяющиеся в неоднородной по
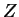 -координате среде, с течением времени сильно вытягиваются.
Особенно это становится заметным при больших градиентах плотности
окружающего газа. При чисто гауссовом распределении газа по
-координате среде, с течением времени сильно вытягиваются.
Особенно это становится заметным при больших градиентах плотности
окружающего газа. При чисто гауссовом распределении газа по
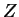 -координате верхняя часть оболочки может ускоряться и в конечном
счете разрушаться под действием неустойчивости Рэлея-Тейлора [41,32].
Игуменщев и др. [32] показали, что в гауссовой атмосфере со шкалой
высот
-координате верхняя часть оболочки может ускоряться и в конечном
счете разрушаться под действием неустойчивости Рэлея-Тейлора [41,32].
Игуменщев и др. [32] показали, что в гауссовой атмосфере со шкалой
высот 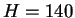 пс эволюционирующая сверхоболочка прорывает газовый диск при
мощности центрального источника энергии
пс эволюционирующая сверхоболочка прорывает газовый диск при
мощности центрального источника энергии
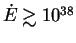 эрг/с. Такое
упрощенное описание вертикального распределения плотности газа позволяет
учесть лишь одну компоненту межзвездной среды -- холодные плотные облачка.
Однако определяющую роль для эффекта прорыва атмосферы могут играть другие
компоненты -- теплый нейтральный и ионизированный газ, горячий газ гало.
Силич и Фомин [95] показали, что точечный взрыв при экспоненциальном
распределении плотности газа с асимптотической ``подложкой''
эрг/с. Такое
упрощенное описание вертикального распределения плотности газа позволяет
учесть лишь одну компоненту межзвездной среды -- холодные плотные облачка.
Однако определяющую роль для эффекта прорыва атмосферы могут играть другие
компоненты -- теплый нейтральный и ионизированный газ, горячий газ гало.
Силич и Фомин [95] показали, что точечный взрыв при экспоненциальном
распределении плотности газа с асимптотической ``подложкой''
![$\rho =
\rho_0\,[\exp (-z/z_0) + \alpha]$](img85.gif) не приводит к эффекту прорыва атмосферы
даже при малых значениях параметра
не приводит к эффекту прорыва атмосферы
даже при малых значениях параметра 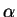 . Роль такой ``подложки'' могут
играть компоненты межзвездной среды с большими характерными полутолщинами.
Кокс [14] указал, что при учете теплого межзвездного газа со шкалой
высот
. Роль такой ``подложки'' могут
играть компоненты межзвездной среды с большими характерными полутолщинами.
Кокс [14] указал, что при учете теплого межзвездного газа со шкалой
высот 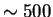 пс, а также давления космических лучей и магнитного поля,
эффект галактических фонтанов получить намного сложнее.
пс, а также давления космических лучей и магнитного поля,
эффект галактических фонтанов получить намного сложнее.
Значительная часть наблюдаемых оболочек кажется вытянутыми не
перпендикулярно плоскости Галактики, а параллельно ей. Этот
феномен можно объяснить влиянием дифференциальности вращения
галактического диска. Тенорио-Таглэ и Палоуш [64] провели
расчеты эволюции оболочек в дифференциально вращающемся
газовом диске галактики. Построенная ими численная двумерная
модель основывалась на приближении тонкого слоя. В работе
рассматривалась цилиндрическая оболочка с начальным радиусом
100 пс и такой же высотой. Предполагалось также, что
невозмущенный газ галактического диска равномерно распределен
в слое с толщиной 100 пс и что оболочка в процессе своей
эволюции уже ``прорвала'' этот слой. Считалось, что верхний и
нижний концы цилиндрической оболочки движутся со скоростью,
равной скорости звука в окружающем газе. Предполагалось
мгновенное выделение всей энергии. Результаты расчетов
показали, что примерно через
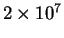 лет вытянутость
оболочек вдоль галактической плоскости становится хорошо
заметной, а при временах, больших
лет вытянутость
оболочек вдоль галактической плоскости становится хорошо
заметной, а при временах, больших 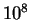 лет, отношение
большой и малой полуосей эллипса достигает 10. В отдельных
вариантах расчетов также учитывалась самогравитация оболочек.
Ее учет приводит к некоторым отличиям лишь при временах,
больших
лет, отношение
большой и малой полуосей эллипса достигает 10. В отдельных
вариантах расчетов также учитывалась самогравитация оболочек.
Ее учет приводит к некоторым отличиям лишь при временах,
больших
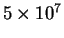 лет. Тенорио-Таглэ и
Палоуш [64] также подчеркнули, что учет
лет. Тенорио-Таглэ и
Палоуш [64] также подчеркнули, что учет 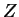 -компоненты
гравитационного поля галактики мог бы существенно повлиять на
их результаты. К тому же очевидно, что представление газового
диска галактики в виде однородного слоя является очень грубым
приближением.
-компоненты
гравитационного поля галактики мог бы существенно повлиять на
их результаты. К тому же очевидно, что представление газового
диска галактики в виде однородного слоя является очень грубым
приближением.
В этой же работе [64] Тенорио-Таглэ и Палоуш впервые
рассмотрели вопрос об образовании молекулярных облаков в
расширяющихся оболочках. Влияние неоднородности распределения
газа по 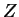 -координате и роль
-координате и роль 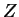 -компоненты гравитационного
поля Галактики не учитывались, поэтому увеличение
поверхностной плотности в оболочке до величины, необходимой
для экранировки внешнего УФ-излучения и образования
молекулярного водорода, было связано только с нагребанием
межзвездного газа и искажением формы оболочки дифференциальным
вращением Галактики. Как будет показано в следующей главе, в
трехмерных оболочках лучевая концентрация увеличивается не
только за счет нагребания окружающего газа и
дифференциальности вращения галактического диска, но и в
результате искажения формы оболочки при ее движении в
неоднородном слое газа под влиянием
-компоненты гравитационного
поля Галактики не учитывались, поэтому увеличение
поверхностной плотности в оболочке до величины, необходимой
для экранировки внешнего УФ-излучения и образования
молекулярного водорода, было связано только с нагребанием
межзвездного газа и искажением формы оболочки дифференциальным
вращением Галактики. Как будет показано в следующей главе, в
трехмерных оболочках лучевая концентрация увеличивается не
только за счет нагребания окружающего газа и
дифференциальности вращения галактического диска, но и в
результате искажения формы оболочки при ее движении в
неоднородном слое газа под влиянием 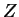 -компоненты
гравитационного поля Галактики. Для понимания этого процесса
необходимо, таким образом, проведение трехмерных расчетов. На
возможность образования молекулярного газа в расширяющихся
оболочках указывали также МакКрэй и Кафатос [45].
Возможность фрагментации оболочек за счет гравитационной
неустойчивости оценивалась в [64,83,45].
-компоненты
гравитационного поля Галактики. Для понимания этого процесса
необходимо, таким образом, проведение трехмерных расчетов. На
возможность образования молекулярного газа в расширяющихся
оболочках указывали также МакКрэй и Кафатос [45].
Возможность фрагментации оболочек за счет гравитационной
неустойчивости оценивалась в [64,83,45].
Бисноватым-Коганом и Силичем [80], Силичем [94,59] и независимо
Палоушем [50,51] была предложена трехмерная численная схема для
расчета эволюции оболочек, основанная на приближении тонкого слоя (т.н.
2.5-мерная газодинамика). В модели учитывалось гравитационное поле
Галактики (по данным Аллена [1]), неоднородность распределения газа по
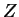 -координате (из работ Локмана и др. [39] и Рейнолдса [56]) и
дифференциальность вращения галактического диска. В качестве начальных
условий были взяты аналитические решения Уивера и др. [72],
описывающие эволюцию оболочки на стадии звездного ветра. Вспышки сверхновых
моделировались в виде квазинепрерывного источника энергии с мощностью от
-координате (из работ Локмана и др. [39] и Рейнолдса [56]) и
дифференциальность вращения галактического диска. В качестве начальных
условий были взяты аналитические решения Уивера и др. [72],
описывающие эволюцию оболочки на стадии звездного ветра. Вспышки сверхновых
моделировались в виде квазинепрерывного источника энергии с мощностью от
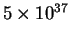 до
до
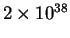 эрг/с. Через несколько десятков
миллионов лет влияние
эрг/с. Через несколько десятков
миллионов лет влияние 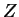 -компоненты гравитационного поля Галактики
приводит к ``оседанию'' значительной части нагребенной массы оболочки на
галактическую плоскость и в конечном итоге к ее разрушению [94]. За
это время дифференциальное вращение не успевает сильно вытянуть оболочку, и
отношение большой и малой полуосей сечения оболочки плоскостью Галактики не
превышает двух. Эти результаты существенно отличаются от полученных
Тенорио-Таглэ и Палоушем [64] в двумерном случае.
-компоненты гравитационного поля Галактики
приводит к ``оседанию'' значительной части нагребенной массы оболочки на
галактическую плоскость и в конечном итоге к ее разрушению [94]. За
это время дифференциальное вращение не успевает сильно вытянуть оболочку, и
отношение большой и малой полуосей сечения оболочки плоскостью Галактики не
превышает двух. Эти результаты существенно отличаются от полученных
Тенорио-Таглэ и Палоушем [64] в двумерном случае.


Следующий: 2. Образование молекулярных облаков
Вверх: 1. Сверхоболочки в нашей
Предыдущий: 1.1 Наблюдательные данные
Sergey Mashchenko
2000-10-25
![]() до
до ![]() лет. Считалось, что оболочка
прекращает свою эволюцию распадаясь на отдельные фрагменты,
когда ее скорость сравнивается со скоростью звука в окружающем
газе
лет. Считалось, что оболочка
прекращает свою эволюцию распадаясь на отдельные фрагменты,
когда ее скорость сравнивается со скоростью звука в окружающем
газе ![]() км/с.
км/с.
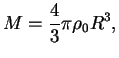
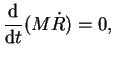
![\begin{displaymath}
n(z) = n_0 \left\{ 0.22 \exp \left[ -\frac{\Phi(z)}{\sigma_...
... 0.78 \exp \left[ -\frac{\Phi(z)}{\sigma_c^2}\right]
\right\}
\end{displaymath}](img77.gif)