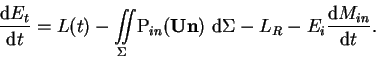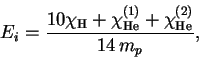

Следующий: 3.2.2 Процедура проекции оболочек
Вверх: 3.2 Численная схема
Предыдущий: 3.2 Численная схема
Для моделирования эволюции сверхоболочки использовалась
описанная в разделе 2.2.1 (с. ![[*]](crossref.gif) )
2.5-мерная численная схема, основанная на приближении тонкого
слоя. Алгоритм был модифицирован с тем, чтобы учесть эффекты
теплопроводности, приводящие к испарению внутренних слоев
холодной плотной оболочки, установлению степенного
распределения температуры и плотности газа вдоль радиуса и
увеличению потерь энергии за счет излучения этого
газа [76,10,72]. Предполагалось, что вскоре после
перехода расширяющейся оболочки в радиационную фазу внутри нее
устанавливается автомодельное распределение температуры вдоль
радиуса (а с учетом постоянства давления в приближении тонкого
слоя -- и распределение плотности газа) [13,40]:
)
2.5-мерная численная схема, основанная на приближении тонкого
слоя. Алгоритм был модифицирован с тем, чтобы учесть эффекты
теплопроводности, приводящие к испарению внутренних слоев
холодной плотной оболочки, установлению степенного
распределения температуры и плотности газа вдоль радиуса и
увеличению потерь энергии за счет излучения этого
газа [76,10,72]. Предполагалось, что вскоре после
перехода расширяющейся оболочки в радиационную фазу внутри нее
устанавливается автомодельное распределение температуры вдоль
радиуса (а с учетом постоянства давления в приближении тонкого
слоя -- и распределение плотности газа) [13,40]:
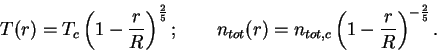 |
(3.1) |
Здесь 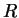 -- расстояние оболочки от центра
остатка. В трехмерном случае темп испарения несферической
оболочки по аналогии с [13,40] моделировался следующим
образом:
-- расстояние оболочки от центра
остатка. В трехмерном случае темп испарения несферической
оболочки по аналогии с [13,40] моделировался следующим
образом:
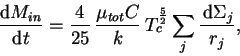 |
(3.2) |
где
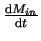 -- масса, испаряемая
оболочкой за единицу времени,
-- масса, испаряемая
оболочкой за единицу времени, 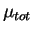 -- средняя масса на
одну частицу плазмы (при 10% по числу частиц содержании гелия
-- средняя масса на
одну частицу плазмы (при 10% по числу частиц содержании гелия
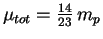 ,
, 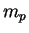 -- масса протона),
коэффициент теплопроводности принимался равным
-- масса протона),
коэффициент теплопроводности принимался равным
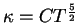 ,
,
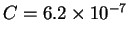 эрг/(с см
эрг/(с см
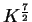 ),
), 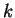 -- постоянная
Больцмана,
-- постоянная
Больцмана,
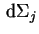 и
и 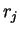 -- площадь лагранжевого
элемента оболочки и его расстояние до центра оболочки. Функция
охлаждения
-- площадь лагранжевого
элемента оболочки и его расстояние до центра оболочки. Функция
охлаждения 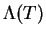 численно интерполировалась по данным
Гаетца и Салпитера [27]. Используя соотношение
численно интерполировалась по данным
Гаетца и Салпитера [27]. Используя соотношение 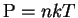 , уравнение состояния идеального газа (предпоследнее
уравнение в системе (2.20) на с.
, уравнение состояния идеального газа (предпоследнее
уравнение в системе (2.20) на с. ![[*]](crossref.gif) ), и
выражение для массы газа внутри оболочки (полученное путем
интегрирования формулы для
), и
выражение для массы газа внутри оболочки (полученное путем
интегрирования формулы для 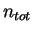 (3.1) по всему
объему остатка), температуру в центре оболочки можно записать
в виде:
(3.1) по всему
объему остатка), температуру в центре оболочки можно записать
в виде:
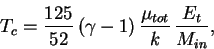 |
(3.3) |
где 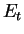 -- тепловая энергия остатка и
-- тепловая энергия остатка и 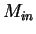 -- полная масса испарившегося газа внутри оболочки
(определяется из решения уравнения 3.2).
-- полная масса испарившегося газа внутри оболочки
(определяется из решения уравнения 3.2).
Энергия, теряемая плазмой на излучение, для произвольной
функции охлаждения 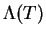 может быть определена по
формуле [11]:
может быть определена по
формуле [11]:
 |
(3.4) |
где 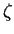 -- металличность. Для солнечного
химсостава концентрация ионов в плазме
-- металличность. Для солнечного
химсостава концентрация ионов в плазме 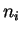 связана с полной
концентрацией
связана с полной
концентрацией 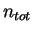
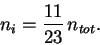 |
(3.5) |
Тогда для случая автомодельного профиля
концентрации (3.1) полные потери на излучение при
остывании горячего газа внутри остатка могут быть записаны в
виде:
![\begin{displaymath}
L_R = \frac{15}{2}\,\zeta n_{i,c}^2 \,\Omega \int\limits_{T...
...\left(\frac{T}{T_c}\right)^{\frac{5}{2}}\right]^2 \,{\rm d} T,
\end{displaymath}](img272.gif) |
(3.6) |
где 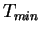 -- минимальная температура, при
которой еще учитываются потери плазмы на излучение (в расчетах
принималось
-- минимальная температура, при
которой еще учитываются потери плазмы на излучение (в расчетах
принималось
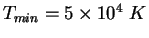 ), и
), и 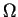 -- объем
оболочки.
-- объем
оболочки.
Уравнение сохранения энергии теперь будет иметь вид (ср.
с (2.4) на с. ![[*]](crossref.gif) )
)
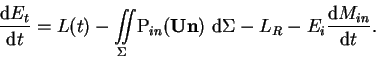 |
(3.7) |
Здесь также учитываются потери на ионизацию
испаряющегося газа (последнее слагаемое). Энергия ионизации на
единицу массы для солнечного содержания гелия:
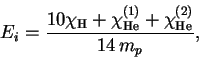 |
(3.8) |
где 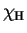 ,
,
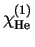 и
и
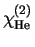 -- потенциалы ионизации водорода,
нейтрального и однократно ионизированного гелия.
-- потенциалы ионизации водорода,
нейтрального и однократно ионизированного гелия.


Следующий: 3.2.2 Процедура проекции оболочек
Вверх: 3.2 Численная схема
Предыдущий: 3.2 Численная схема
Sergey Mashchenko
2000-10-25
![[*]](crossref.gif) )
2.5-мерная численная схема, основанная на приближении тонкого
слоя. Алгоритм был модифицирован с тем, чтобы учесть эффекты
теплопроводности, приводящие к испарению внутренних слоев
холодной плотной оболочки, установлению степенного
распределения температуры и плотности газа вдоль радиуса и
увеличению потерь энергии за счет излучения этого
газа [76,10,72]. Предполагалось, что вскоре после
перехода расширяющейся оболочки в радиационную фазу внутри нее
устанавливается автомодельное распределение температуры вдоль
радиуса (а с учетом постоянства давления в приближении тонкого
слоя -- и распределение плотности газа) [13,40]:
)
2.5-мерная численная схема, основанная на приближении тонкого
слоя. Алгоритм был модифицирован с тем, чтобы учесть эффекты
теплопроводности, приводящие к испарению внутренних слоев
холодной плотной оболочки, установлению степенного
распределения температуры и плотности газа вдоль радиуса и
увеличению потерь энергии за счет излучения этого
газа [76,10,72]. Предполагалось, что вскоре после
перехода расширяющейся оболочки в радиационную фазу внутри нее
устанавливается автомодельное распределение температуры вдоль
радиуса (а с учетом постоянства давления в приближении тонкого
слоя -- и распределение плотности газа) [13,40]:
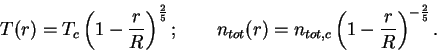
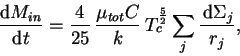

![\begin{displaymath}
L_R = \frac{15}{2}\,\zeta n_{i,c}^2 \,\Omega \int\limits_{T...
...\left(\frac{T}{T_c}\right)^{\frac{5}{2}}\right]^2 \,{\rm d} T,
\end{displaymath}](img272.gif)