
 |
 |
| MAIN | BIOGRAPHY | PUBLICATIONS | RESEARCH AREA | TEACHING | GROUP MEMBERS & PROJECTS |
Quantum catastrophes and caustics |
|---|
The places where a physical theory breaks down are perhaps its most interesting parts because they indicate the need for new physics. A well known example of this is at a black hole where general relativity predicts a singularity. It is believed that such a singularity may be tempered by introducing quantum mechanics into the theory of gravity which is a major, but as yet inconclusive, area of research. |
The cusp is the second in Thom's hierarchy of catastrophes and gives the universal shape of structurally stable singularities in a plane. Left: each layer of the cubic surface represents a family of rays. Above each point in the (C1,C2) plane, which here corresponds to physical space, there are either one or three layers meaning that either one or three rays pass through that point. Two rays coalesce at the cusp boundary and all three solutions coalesce at the cusp point. Centre: the cusp caustic in a coffee cup is an everyday example. Right: The geometric ray theory of caustics (involutes) has been studied for a long time, in this case by Leonardo da Vinci around 1508. (Figs. (a) and (b) are from our paper on caustics in spin systems and Josephson junctions, and the sketch by da Vinci is held by the British Library, codex Arundel 263, folio 87v, see also this article.) |
|
At a more everyday level, singularities are common in optics where they are known as caustics. Examples include the bright lines on the bottom of swimming pools and coffee cups, rainbows, and the twinkling of starlight. Caustics are regions of focusing where the ray theory of light predicts infinite intensity and one must go to the the next level of sophistication, namely wave theory, to obtain a well behaved result. Remarkably, the singularities that occur in physical theories based on a minimum principle (essentially the whole of classical and quantum mechanics, electromagnetism, etc.) often take on certain characteristic shapes such as the cusp shown above. In the 1970s it was realized (notably by Vladimir Arnold, Michael Berry, and John Nye) that the natural mathematical language to describe caustics is catastrophe theory. More precisely, catastrophe theory studies structurally stable singularities which means that they are stable against perturbations and hence survive in the wild. |
The wave catastrophe for the cusp. The diverging amplitude found in the ray caustic has been removed and replaced by an interference pattern (Pearcey function). However, the dots mark phase singularities which come in vortex-antivortex pairs. (Figure is from our paper on light cones). |
|
The new physical concept in wave theory in comparison to ray theory is phase. This gives rise to interference patterns, known as wave catastrophes, that dress caustics at the wavelength scale. In the case of the cusp the wave function is a complex function of two variables known as the Pearcey function. Wave catastrophes can be expressed as diffraction integrals and are tabulated in the NIST Digital Library of Mathematical Functions. However, as indicated in the figure above, although the interference pattern does not suffer from any divergences of the wave amplitude, at its finest scales it is made up of a network of nodes (zeros). These turn out to be vortices about which the phase winds: at the centre of each vortex the phase is undefined because it takes all values. Therefore, the introduction of wave theory has tamed one singularity but introduced another.
My group's research is on the next generation of these objects, namely quantum catastrophes (not to be confused with the song by the death metal band Brain Drill). It turns out that phase is a rather subtle concept: it is an emergent quantity which is poorly defined at the quantum level only becoming sharp in the semiclassical regime where the wave amplitude is large, giving us a big hint as to what remedy should be applied. Following the pattern set out above, the regularization of phase singularities can be achieved by going to the next level of sophistication which is quantum field theory: the discretization of a field removes phase singularities. |
 |
 |
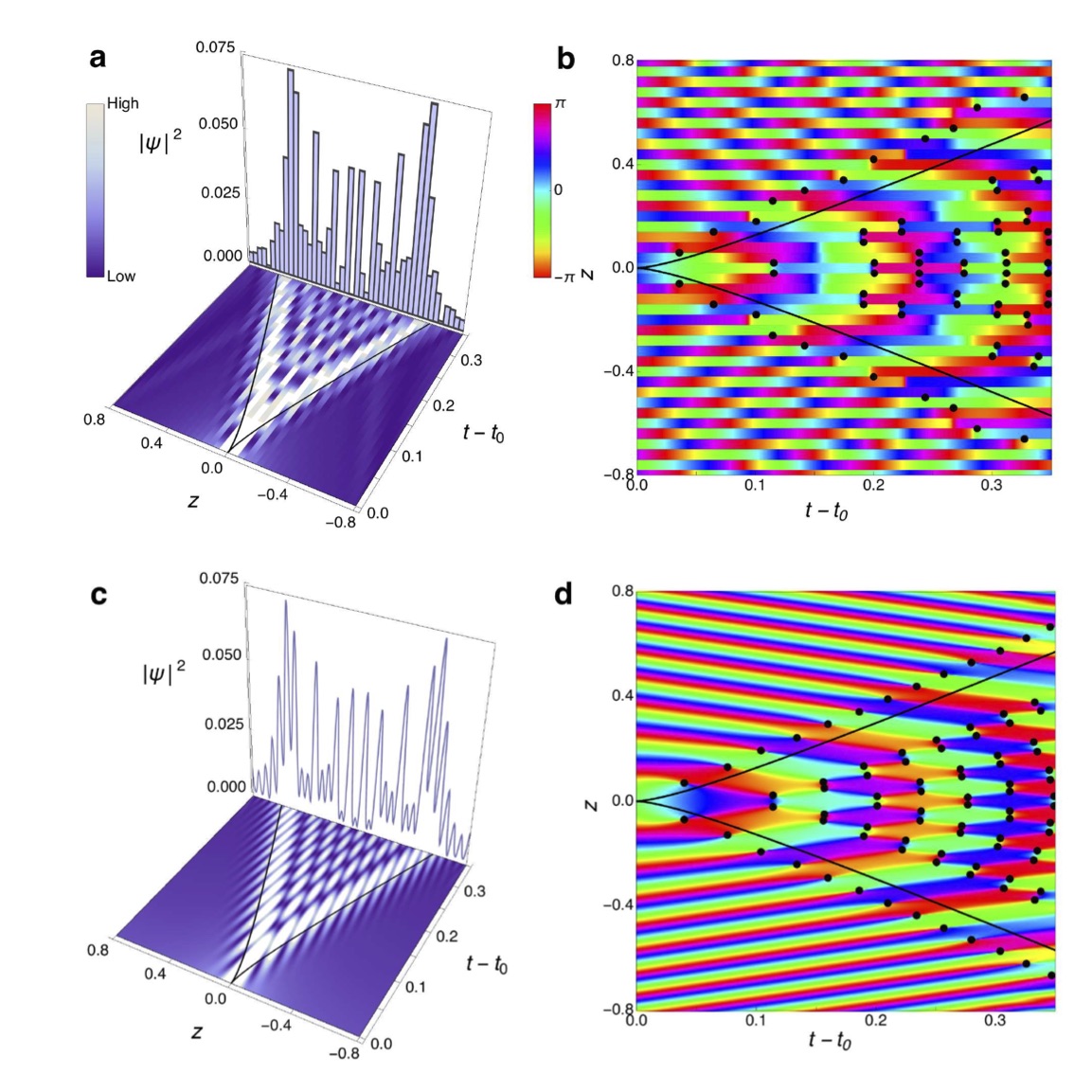
A quantum catastrophe versus a wave catastrophe.
The upper left two panels show the amplitude and phase for a quantum cusp
(discrete version of Pearcey function) whereas the lower left two panels show the continuous version
(Pearcey function). The diverging amplitude found
in the ray version has been removed by interference and the phase singularities in the wave catastrophe
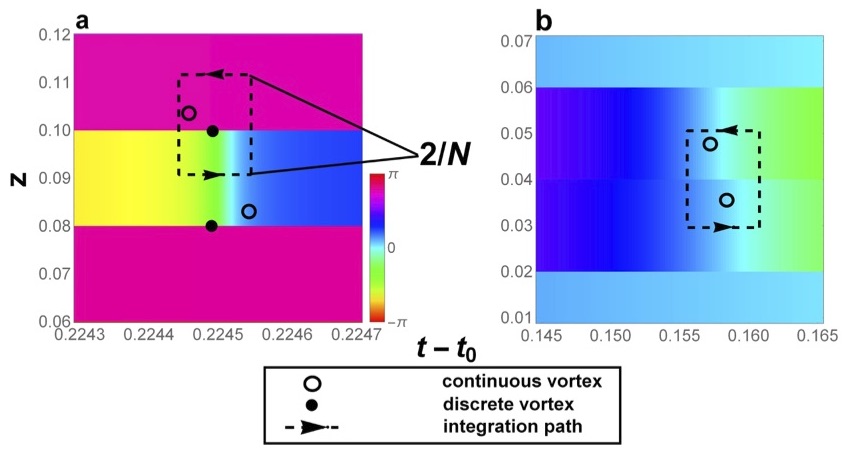
have been removed by discretization. The right hand two panels show zoom-ins of two vortex-antivortex pairs
in the discrete case. The discretization of the quantum amplitudes in a quantum field means that vortices become
non-local and phase singularities can no longer occur. The cusp shown in these figures is actually in
Fock space
which is the natural domain for quantum field theories. It is generated by the collective
dynamics following a quench in a spin
system with long-range interactions, or equivalently, two coupled Bose-Einstein condensates.
Similar structures occur in coordinate space on a
spin chain.
| ||||
|
The point of view taken in the above description of ray and wave catastrophes/caustics
is essentially that espoused in Michael Berry's review
Singularities in Waves and Rays in Les
Houches, Session XXXV, 1980 Physics of Defects,
edited by R. Balian et al. (North-Holland Publishing, Amsterdam, 1981). Ulf Leonhardt has pointed out that
Hawking radiation from a black hole
can be interpreted as a quantum catastrophe.
|
Overview of ultra-cold atoms |
|---|
Ultracold atoms are an area of research which began with the development of the technique of laser cooling (1997 Nobel prize in Physics for Chu, Cohen-Tannoudji and Phillips). Laser cooling allows one to cool atoms down to some millionths of a degree above absolute zero, they can then be held in atom traps made from electromagnetic fields and/or `optical lattices’ made from the interference of two or more laser beams. In this second configuration the atoms are analogous to electrons in a crystal lattice like those found in a metal, but with (at least) three crucial differences:
Cold atoms can therefore be used to investigate single- and many-particle quantum mechanics in a system that can be stripped down to the bare essentials. A good example is the superfluid to Mott insulator transition (the Mott insulator state is believed by some people to play a role in high-temperature superconductivity), which was observed in atoms in an optical lattice in 2002 [Greiner et al, Nature 415, 39 (2002)]---see figure. At a particular ratio between the lattice depth and the interaction strength the atoms undergo an abrupt change from being in a superfluid state, with the atoms delocalized across the lattice, to suddenly having exactly one atom per site with highly suppressed fluctuations. This is an example of a so-called quantum phase transition between different ground states of a many-particle system, in this case between a coherent state, where each atom is in a superposition of being on many different sites, and a Fock state of exactly one per site.
A Bose-Einstein condensate (BEC) is a quantum-coherent state of matter in which every atom is in the same quantum state. From an AMO perspective a BEC is to atoms what a laser is to photons. Lasers were pure research in the 1950s and1960s but nowadays they are found in a tremendous range of technology from communications (e.g. the light in optical fibres) to medicine to CD players and supermarket checkouts. Coherent matter-wave optics based on BECs (where all the atomic de Broglie waves are in phase) is just starting out, but is rapidly becoming a very active research area. One reason for all the excitement is that the wavelength of atoms can be orders of magnitude smaller than that of light and so an interferometer based on atoms has the potential to be much more sensitive. Another very important difference is that atoms interact quite differently with their environment than photons. For example, atoms couple directly to the gravitational field and so can be a sensitive measure of gravity. It may come as a surprise to learn that, although gravity has been intensively studied on large length scales, the situation at short length scales, below about a millimeter, is comparatively unknown. Atomic interferometers hold out the possibility of making exquisitely sensitive measurements of the gravitational field at very small distances from an object. Such measurements might have far-reaching consequences since string theory, the current most fundamental but as yet untested theory of `everything’, predicts extra dimensions which can soak up gravitons and thus weaken gravity on small scales [see Lisa Randall, Warped Passages: Unraveling The Mysteries Of The Universe's Hidden Dimensions (Ecco, New York, 2005)].
|