3.2.2 Процедура проекции оболочек на картинную плоскость

В результате численных расчетов получаются координаты, скорости и лучевые концентрации HI в лагранжевых элементах, представляющих собой различные элементы движущейся оболочки. Для сравнения результатов численного моделирования с наблюдениями необходимо найти распределение лучевой концентрации HI (с учетом вкладов оболочки и окружающего галактического газа) в картинной плоскости. На поздних стадиях эволюции оболочка приобретают сложную трехмерную форму, и для сравнения с наблюдениями необходимо развить процедуру ее численного проектирования на картинную плоскость.

Для выполнения этой операции перейдем от галактической системы координат (

) к системе координат (

), связанной с картинной плоскостью. Эти системы координат вводятся таким образом, чтобы их центры совпадали с динамическим центром галактики, оси

совпадали с линией узлов и были направлены от приближающегося к нам к удаляющемуся краю галактики. Ось

направлена вдоль вектора углового момента вращения галактики, а ось

-- вдоль луча зрения к наблюдателю. Тогда

где

-- угол между осями

. Угол

равен либо углу наклона галактики

(который заключен в пределах от $0^{\circ}$ до $90^{\circ}$ ), либо равен $i' = 180^{\circ}-i$ , в зависимости от того, как направлен вектор углового момента вращения галактики. Лучевая концентрация вдоль произвольного луча зрения равна сумме вкладов оболочки и невозмущенного газа галактики:

**Рисунок 3.1:** Схема для вычисления лучевой концентрации
$\begin{figure}\begin{picture}(6.693,2.88) \put(2.317,2.88){\special{em:graph MNf1}} \end{picture}\end{figure}$

где индекс

нумерует лагранжевые элементы оболочки, пересекаемые лучом зрения,

-- вклад каждого такого элемента в полную лучевую концентрацию, последнее слагаемое дает вклад в лучевую концентрацию галактического невозмущенного газа. Величина

определяется по лучевой концентрации оболочки с учетом толщины оболочки и угла $\alpha$ между лучом зрения и нормалью к поверхности оболочки (рис. 3.1).

В приближении тонкого слоя толщина оболочки не может быть определена из основных уравнений метода. Поэтому мы вводим величину

, которая приближенно учитывает термодинамику оболочки и влияние межзвездного магнитного поля [44]. Предполагается, что относительная толщина $\delta=d/R_s$ является константой вдоль поверхности оболочки и не меняется с течением времени. Заменяя лагранжевый элемент сферическим сегментом с радиусом $R_{s,j}$ и толщиной

, можно оценить лучевую концентрацию как

$\begin{displaymath} N_l=\frac{N_{s,l}}{\delta}\times \left\{ {F_1(\alpha,\delta)... ...pha,\delta)\,,\hspace{1.16cm} \alpha \ge \alpha_{cr},} \right. \end{displaymath}$

(3.11)

$\displaystyle F_1(\alpha,\delta)$	$\textstyle =$	$\displaystyle \sqrt{\cos^2\alpha+\delta+\frac{\delta^2}{4}},$	(3.12)
$\displaystyle F_2(\alpha,\delta)$	$\textstyle =$	$\displaystyle \sqrt{\cos^2\alpha-\delta+\frac{\delta^2}{4}},$	(3.13)

и критический угол между лучом зрения и нормалью к поверхности $\alpha_{cr}$ определяется как $\sin \alpha_{cr}=1-\delta /2$ . Для учета сглаживающего эффекта углового разрешения радиотелескопа и значительной толщины оболочки на поздних дозвуковых стадиях эволюции в расчетах принималось значение $\delta=0.2$ [70]. Эта приближенная процедура сглаживает распределение лучевой концентрации возле краев HI дыр, но не оказывает значительного влияния на дальнейший анализ. (Как будет показано в следующей главе, строгий учет сглаживающего влияния углового разрешения радиотелескопа приводит к аналогичным результатам).

**Рисунок 3.2:** Изображение спроектированной оболочки в галактике М31 для кпс, $L=10^{38}$ эрг/с, млн. лет, $\theta =70^{\circ }$ . Контурные линии соответствуют лучевым концентрациям 2.0, 2.1, 2.2, 2.4, 2.5, 2.6, 2.7, 2.8, 3.1, 3.4, 3.7, 4.0 в единицах $10^{21}~$ см $^{-2}$ . Толстая линия соответствует лучевой концентрации по уровню 50% $2.3\times 10^{21}~$ см $^{-2}$ .
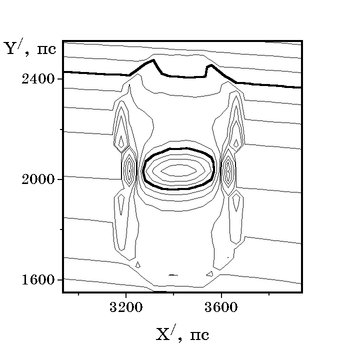$\begin{figure}\begin{picture}(6.693,2.333) \put(2.18,2.333){\special{em:graph MNf2}} \end{picture}\end{figure}$

**Рисунок 3.3:** Схематическое представление ориентации дыры HI в картинной плоскости.
$\begin{figure}\begin{picture}(6.693,2.333) \put(2.18,2.333){\special{em:graph MNf3}} \end{picture}\end{figure}$

На рис. 3.2 изображена типичная рассчитанная карта распределения лучевой концентрации HI в окрестностях сверхоболочки, расположенной на расстоянии 10 кпс от центра галактики М31 после 10 млн. лет эволюции. Предполагалось, что изоденса с уровнем 50% соответствует наблюдаемой границе дыры в распределении HI (на рисунке -- толстая линия). Такая изоденса для каждой полученной карты лучевых концентраций аппроксимировалась эллипсом, и таким образом определялись параметры области с дефицитом HI (большая и малая оси, и ориентация эллипса в картинной плоскости). Ориентация определяется углом $\varphi$ между большой осью эллипса и направлением на центр галактики в картинной плоскости, как показано на рис. 3.3.

		$\displaystyle x'=x,$
		$\displaystyle y'=y\cos i'+z\sin i',$	(3.9)
		$\displaystyle z'=-y\sin i'+z\cos i',$