

Следующий:3.3.2
Входные параметрыВверх:3.3.1
Модели галактикПредыдущий:3.3.1.1
Неправильная галактика HoII
3.3.1.2 Спиральная галактика
M31
Галактика М31, расположенная от нас на расстоянии 690 кпс, имеет массу
и размеры, близкие к нашей Галактике, и является ближайшей к нам спиральной
системой. Радионаблюдения [5] обнаружили в
этой системе 141 дыру в распределении HI. Большинство из них расположены
на галактоцентрических расстояниях 10-15 кпс.
Кривая вращения М31 может быть хорошо описана в рамках двухкомпонентной
(диск + балдж) массовой модели с массой диска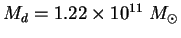 и массой балджа
и массой балджа 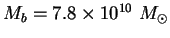 [4]. Распределение массы в галактике моделировалось
как сумма двухэкспоненциального диска (в
[4]. Распределение массы в галактике моделировалось
как сумма двухэкспоненциального диска (в 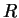 и
и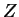 направлении) и сферического балджа [16]:
направлении) и сферического балджа [16]:
где характерная шкала длин в диске составляет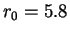 кпс, и параметр балджа
кпс, и параметр балджа 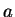 равен
равен 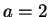 кпс [71]. Для
кпс [71]. Для 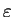 было принято значение
было принято значение 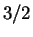 [16], и предполагалось такое же отношение
характерных шкал
[16], и предполагалось такое же отношение
характерных шкал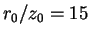 ,
как и для случая нашей Галактики [38], что
дает значение параметра
,
как и для случая нашей Галактики [38], что
дает значение параметра 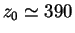 пс.
пс.
Гравитационный потенциал галактики может быть записан как
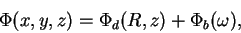 |
(3.20) |
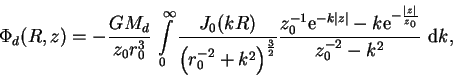 |
(3.21) |
![\begin{displaymath}\Phi_b (\omega)=\frac{G M_b}{a} \frac{1}{2-\varepsilon} \lef...... +a}\right)^{2-\varepsilon}-1\right],\quad \varepsilon\ne 2.\end{displaymath}](img353.gif) |
(3.22) |
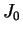 -- функция Бесселя. В предположении вращательного равновесия центробежная
сила уравновешивается гравитационной силой, и круговая скорость газовой
компоненты
-- функция Бесселя. В предположении вращательного равновесия центробежная
сила уравновешивается гравитационной силой, и круговая скорость газовой
компоненты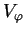 может быть выражена как
может быть выражена как
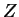 -компонента
гравитационного поля вычислялась численно по формуле:
-компонента
гравитационного поля вычислялась численно по формуле:
Несмотря на большой угол наклона М31, вертикальное распределение газовой
плотности все еще плохо известно. Поэтому предполагалось гидростатическое
равновесие с политропой ![${\rm P}={\rm P}_0 \, [\rho(z)/\rho_0]^{\lambda}$](img366.gif) ,
что дает вертикальное распределение газовой плотности
,
что дает вертикальное распределение газовой плотности
![\begin{displaymath}\rho (z)=\rho_0 \left\{1-\frac{\lambda-1}{\lambda} \frac{\rh......}\left[\Phi (z)-\Phi_0\right] \right\}^{\frac{1}{\lambda-1}},\end{displaymath}](img367.gif) |
(3.29) |
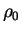 ,
, 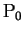 ,
, 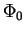 -- значения газовой плотности, давления газа и гравитационного потенциала
вблизи плоскости галактики. Температура невозмущенного газа увеличивается
с расстоянием до галактической плоскости как
-- значения газовой плотности, давления газа и гравитационного потенциала
вблизи плоскости галактики. Температура невозмущенного газа увеличивается
с расстоянием до галактической плоскости как
![\begin{displaymath}T(z)=\frac{\mu}{k} \frac{{\rm P}_0}{\rho_0} \left[ \frac{\rho(z)}{\rho_0}\right]^{\lambda-1}.\end{displaymath}](img370.gif) |
(3.30) |
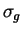 является почти постоянной величиной, и меняется от 7 км/с до 10 км/с [7].
Для М31 она равна 8.1 км/с [69], и не показывает
зависимости от галактоцентрического расстояния. Для грубой оценки параметров
является почти постоянной величиной, и меняется от 7 км/с до 10 км/с [7].
Для М31 она равна 8.1 км/с [69], и не показывает
зависимости от галактоцентрического расстояния. Для грубой оценки параметров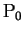 ,
, 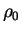 ,
и
,
и 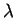 предполагается, что
предполагается, что 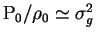 .
Принимая наличие горячего галактического гало с температурой
.
Принимая наличие горячего галактического гало с температурой 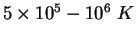 при
при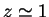 кпс, и сравнивая поверхностную плотность, получаемую путем интегрирования
уравнения (3.29), можно оценить индекс политропы
как
кпс, и сравнивая поверхностную плотность, получаемую путем интегрирования
уравнения (3.29), можно оценить индекс политропы
как 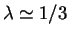 .
В такой модели температура в плоскости галактики не меняется с галактоцентрическим
расстоянием, и равна
.
В такой модели температура в плоскости галактики не меняется с галактоцентрическим
расстоянием, и равна 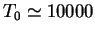 K. Металличность оценивалась по эмпирической зависимости [33]:
K. Металличность оценивалась по эмпирической зависимости [33]:
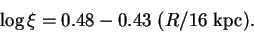 |
(3.31) |


Следующий:3.3.2
Входные параметрыВверх:3.3.1
Модели галактикПредыдущий:3.3.1.1
Неправильная галактика HoII
Sergey Mashchenko 2000-10-25
![]() и массой балджа
и массой балджа ![]() [4]. Распределение массы в галактике моделировалось
как сумма двухэкспоненциального диска (в
[4]. Распределение массы в галактике моделировалось
как сумма двухэкспоненциального диска (в ![]() и
и![]() направлении) и сферического балджа [16]:
направлении) и сферического балджа [16]:
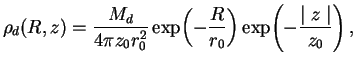
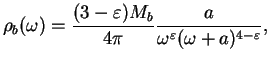
![]() кпс, и параметр балджа
кпс, и параметр балджа ![]() равен
равен ![]() кпс [71]. Для
кпс [71]. Для ![]() было принято значение
было принято значение ![]() [16], и предполагалось такое же отношение
характерных шкал
[16], и предполагалось такое же отношение
характерных шкал![]() ,
как и для случая нашей Галактики [38], что
дает значение параметра
,
как и для случая нашей Галактики [38], что
дает значение параметра ![]() пс.
пс.
![$\displaystyle \sqrt{R\left[\left(\frac{\partial \Phi_d}{\partial R}\right)^2_{...... z=0}+\left(\frac{\partial \Phi_b}{\partial R}\right)^2_{\!\! z=0}\right]}\,,$](img357.gif)
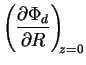
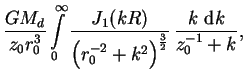
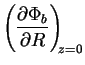
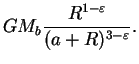
![]() -компонента
гравитационного поля вычислялась численно по формуле:
-компонента
гравитационного поля вычислялась численно по формуле:
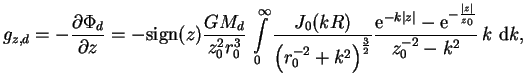
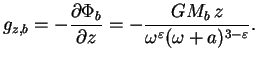
![]() ,
что дает вертикальное распределение газовой плотности
,
что дает вертикальное распределение газовой плотности